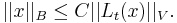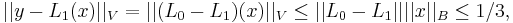Method of continuity
In the mathematics of Banach spaces, the method of continuity provides sufficient conditions for deducing the invertibility of one bounded linear operator from that of another, related operator.
Contents |
Formulation
Let B be a Banach space, V a normed vector space, and ![(L_t)_{t\in[0,1]}](/2012-wikipedia_en_all_nopic_01_2012/I/763582dadada8b0a90cad820c731e6d8.png) a norm continuous family of bounded linear operators from B into V. Assume that there exists a constant C such that for every
a norm continuous family of bounded linear operators from B into V. Assume that there exists a constant C such that for every ![t\in [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/d9a06fde4663cdd5b1ba693e9127232f.png) and every
and every 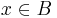
Then 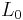 is surjective if and only if
is surjective if and only if 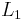 is surjective as well.
is surjective as well.
Applications
The method of continuity is used in conjunction with a priori estimates to prove the existence of suitably regular solutions to elliptic partial differential equations.
Proof
We assume that 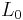 is surjective and show that
is surjective and show that 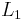 is surjective as well.
is surjective as well.
Subdividing the interval [0,1] we may assume that 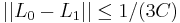 . Furthermore, the surjectivity of
. Furthermore, the surjectivity of 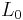 implies that V is isomorphic to B and thus a Banach space. The hypothesis implies that
implies that V is isomorphic to B and thus a Banach space. The hypothesis implies that 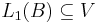 is a closed subspace.
is a closed subspace.
Assume that 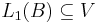 is a proper subspace. The Hahn-Banach theorem shows that there exists a
is a proper subspace. The Hahn-Banach theorem shows that there exists a 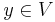 such that
such that 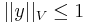 and
and 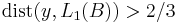 . Now
. Now 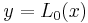 for some
for some 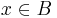 and
and 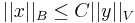 by the hypothesis. Therefore
by the hypothesis. Therefore
which is a contradiction since 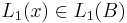 .
.
See also
Sources
- Gilbarg, D.; Trudinger, Neil (1983), Elliptic Partial Differential Equations of Second Order, New York: Springer, ISBN 3-540-41160-7